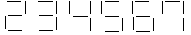|
(Dessin réalisé au primaire) Contactez-moi : cejean@charleries.net |
Les charleries Bienvenue sur mon blogue, Ce blogue contient des souvenirs, des anecdotes, des opinions, de la fiction, des bribes d’histoire, des récréations et des documents d’archives. Charles-É. Jean
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Divertissements mathématiques |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7465
7 janvier 2026
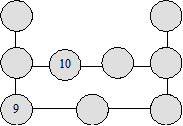
Une corbeille de
biscuits
Lors d’une fête au village, le boulanger décide d’offrir
une grande corbeille de biscuits à un groupe d’enfants.
En partageant la corbeille également entre eux,
chaque enfant reçoit 11 biscuits.
Mais voilà qu’au dernier moment,
deux enfants arrivent en courant.
En partageant alors la même corbeille entre tout le monde,
chaque enfant ne reçoit plus que 10 biscuits.
Combien d’enfants étaient présents au départ ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7464
7 janvier 2026
Pion de Rosalie
Rosalie pose
un pion sur la case 1 de la grille. Cette pièce se déplace en deux
mouvements qui se font en alternance. Le premier mouvement est celui
du cavalier aux échecs, soit en L. Le deuxième mouvement est un pas
horizontal ou vertical. Les quatre premières cases atteintes sont
indiquées.
À la suite de
4, trouvez un chemin qui permet au pion d’atteindre toutes les
cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7463
7 janvier 2026
Grille d’Élodie
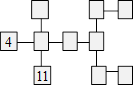
Élodie veut
placer chacun des nombres de 1 à 16 dans la grille. Dans chaque
rangée horizontale, verticale et diagonale, la somme doit être 34.
Les nombres hors de la grille sont la somme des deux
nombres voisins de la même rangée. Le 12 et le 13 sont en
bonne position.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
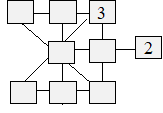
# 7462
7 janvier 2026
Indices de Jonathan
Jonathan a composé une grille qui contient des
nombres différents de 5 à 13. La somme des nombres dans chaque
rangée horizontale et verticale est 27. Certaines valeurs sont
données.
Remplissez la grille avec des nombres.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7461
7 janvier 2026
De bond en bon
Claire a écrit cette addition. Chaque lettre
représente un chiffre différent. On sait que B = 6 et R = 9. Il n’y a pas
de zéro.
B O N D
+
B O N
F I E R
Quelle est la somme ?
Solution. L’égalité est : 6581 + 658 = 7239.
La somme est 7239. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7440
3 décembre 2025
Marche d’une bague
Marthe pose
une bague sur la case 1 de la grille. Cette bague se déplace en deux
mouvements qui se font en alternance. Le premier mouvement
est celui du cavalier aux échecs, soit en L. Le deuxième mouvement
est un pas horizontal ou vertical. Les quatre premières cases
atteintes sont indiquées.
À la suite de
4, trouvez un chemin qui permet à la bague d’atteindre toutes les
cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7439
3 décembre 2025
Figure de Juliette
Juliette a inscrit 1
et 2 dans la grille. Elle veut y placer chacun des nombres de 4 à 8.
La somme doit être 13 dans chaque rangée horizontale et verticale de
trois cases.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7438
3 décembre 2025
Signes de Toussaint
Toussaint veut placer un signe entre les chiffres sans en changer
l’ordre. Le résultat doit être 6.
Insérez les signes appropriés. Utilisez les parenthèses au besoin.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7437
3 décembre 2025
Port de mer
Vite, tous les invités doivent se rendre au port de mer. Dans
l’addition ci-après, chaque lettre représente un chiffre différent.
On sait que M = 6 et E = 8. Chaque case colorée doit recevoir un
chiffre impair.
Quelle est la somme ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7436
3 décembre 2025
Cavalier de Vincent
Vincent pose un cavalier sur la case 1 de la grille. Cette pièce se
déplace en L comme le cavalier aux échecs. Les quatre premières
cases atteintes sont indiquées.
À
la suite de 4, trouvez un chemin qui permet au cavalier d’atteindre
toutes les cases, sauf la noire.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7415
29 octobre 2025
Grille de Marianne
Marianne doit écrire chacun des chiffres de 1 à 9 dans cette grille.
La somme de certaines rangées est donnée à droite et en dessous.
Trois chiffres sont en bonne position.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7414
29 octobre 2025
Dés de Philippe
Philippe est impressionné par le chiffre 7. Par
exemple, il sait que la somme des deux marques sur les faces
opposées d’un dé est 7. Aujourd’hui, il écrit cinq fois le chiffre
7.
À l’aide d’opérations simples, représentez 4 avec
cinq 7.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7413
29 octobre 2025
Défi de Coralie
Coralie lance un défi à son frère :
« Tu dois trouver trois nombres de trois chiffres.
Chacun des chiffres de 1 à 9 doit être utilisé une
seule fois.
La somme de ces trois nombres doit donner 1800.
Et le dernier chiffre de l’un des trois nombres doit
être 1.
Le deuxième chiffre d’un autre nombre doit être 8. »
Trouvez un des trios possibles.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7412
29 octobre 2025
Cavalier de Mario
Mario
pose un cavalier sur la case 1 de la grille. Cette pièce se déplace
en L comme le cavalier aux échecs. Les six premières cases atteintes
sont indiquées.
À partir de 6, trouvez un chemin qui permet au
cavalier d’atteindre toutes les cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7411
29 octobre 2025
Addition d’Adèle
Adèle a écrit l’addition ci-après dont la somme est 159.
Remplacez un chiffre par 1 et un autre par 2 pour obtenir une somme
de 105.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7390
24 septembre 2025
Jetons
de Jeannot
Jeannot prend huit jetons numérotés de 1 à 8. Il désire placer cinq
jetons dans les cases de façon à avoir la même somme dans les deux
diagonales.
Quelle est la plus grande somme possible ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7389
24 septembre 2025
Au bout des doigts
Trois amis ont reçu au total 80 courriels au cours d’une semaine.
Octave en a reçu trois fois plus que Wilfrid.
Augustin en a reçu trois de plus qu’Octave.
Combien chacun a-t-il reçu de courriels ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7388
24 septembre 2025
Cavalier de Bianca
Bianca pose un cavalier sur la case 1 de la grille. Cette pièce se
déplace en L comme le cavalier aux échecs. Les quatre premières
cases atteintes sont indiquées.
À
la suite de 4, trouvez un chemin qui permet au cavalier d’atteindre
toutes les cases, sauf la noire.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7387
24 septembre 2025
En mariage
Rolande a écrit MARIAGE sous forme d’une égalité.
Chaque lettre représente un chiffre différent.
Rolande veut bien nous informer que M = 5 et I = 7.
MA + RI = AGE
Quelle
est la somme ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7386
24 septembre 2025
Grille d’Alexandra
Alexandra veut placer chacun des nombres de 1 à 15
dans cette grille. La somme des nombres de chaque ligne doit être 40
et celle de chaque colonne 24. Tout nombre hors de la grille est la
somme des 2 nombres voisins dans cette rangée.
Remplissez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7365
21 mai 2025
Opérations de Léonard
Léonard choisit le nombre 40. Il fait les opérations indiquées dans
le tableau. À la fin, il obtient 31.
En partant de 42, faites les mêmes opérations, mais dans un autre
ordre, pour obtenir 41.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7364
21 mai 2025
Noix en lignes
Sara a placé 20 noix dans cette figure. Elle veut connaître le
nombre de rangées de 3 noix disposées en ligne droite obliquement.
Une noix peut appartenir à plus d’une rangée.
Combien peut-on compter de rangées obliques ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
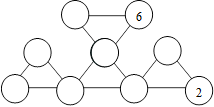
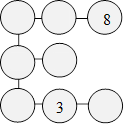
# 7363
21 mai 2025
Triangles d’Alice
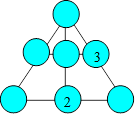
Alice a écrit 2 et 6 dans la figure. Elle veut y placer chacun des
nombres de 4 à 10. La somme des 3 nombres sur les sommets de chaque
triangle doit être 19.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7362
21 mai 2025
Marche d’un canard
Angéla pose un canard sur la case 1 de la grille. Ce canard se
déplace en 2 mouvements qui se font en alternance. Le premier
mouvement est celui du cavalier aux échecs, soit en L. Le deuxième
mouvement est un pas diagonal. Les 5 premières cases atteintes sont
indiquées.
À la suite de 5, trouvez un chemin qui permet au canard d’atteindre
toutes les cases, sauf les noires.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7361
21 mai 2025
Pour des nouvelles
Le 15 juin, Philippe envoie un courriel à 3 de ses proches.
Il promet d’envoyer un courriel
·
à son père tous les 3 jours
·
à sa mère tous les 4 jours
·
à sa sœur tous les 5 jours.
Quand, par la suite, Philippe enverra-t-il un courriel le même jour
à ces personnes ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7340
16 avril 2025
Initiale de Manon
Manon a écrit l’égalité ci-après dans laquelle chacune des trois
lettres a sa propre valeur. Aucune lettre n’est égale à 0.
Trouvez les valeurs possibles de M, considérant que PN est un nombre
de deux chiffres.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7339
16 avril 2025
Jetons de Sofia
Sofia prend huit jetons numérotés de 1 à 8. Elle veut les placer
dans les cellules. La somme doit être 13 dans chaque rangée de 3
cellules reliées par une droite. Le 4 et le 6 sont en bonne
position.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7338
16 avril 2025
De 3 à 100
Denise a représenté 100 avec sept 3. Voici ce qu’elle a écrit :
33/3 × 3 × 3 + 3/3 = 100
Trouvez une autre façon de représenter 100 avec sept 3 et avec au
moins un signe de soustraction.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7337
16 avril 2025
Magie de Diane
Diane a construit un carré magique d'ordre 4 avec les nombres de 1 à
16. La somme de deux cases marquées par une même lettre est égale à
17. La somme de chaque ligne, colonne et diagonale est 34. On sait
que le premier F est 13 et que le deuxième D est 3.
Trouvez un carré magique possible.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7336
16 avril 2025
Signes de Martin
Martin a placé cinq jetons en ligne. Il doit insérer un signe entre
les jetons sans en changer l’ordre. Le résultat doit être 21.
Disposez des signes en faisant chaque calcul à la suite sans se
préoccuper de la priorité des opérations.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7315
12 mars 2025
Cartes de Philéas
Philéas a choisi 4 cartes de pique de valeurs A, B, C et D.
La somme totale des valeurs est 22.
La somme des valeurs de A et de B est celle de C.
La somme des valeurs de B et de C est 12.
La somme des valeurs de C et de D est 3 fois celle de B.
Quelles sont les 4 cartes ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7314
12 mars 2025
Carré d’Alfred
Dans la grille, Alfred a écrit quatre 8. Il veut ajouter quatre 10,
quatre 12 et quatre 14. La somme doit être 44 horizontalement,
verticalement et dans chacune des deux diagonales.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7313
12 mars 2025
Magie de Bastien
Bastien veut placer chacun des nombres de 1 à 11 dans cette figure.
La somme des nombres doit être 15 dans chaque rangée de 3 cellules
reliées par une droite. Quatre nombres sont en bonne position.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7312
12 mars 2025
Grille de Sandrine
Sandrine a dessiné la grille ci-après dans laquelle elle a noirci
des cases. Elle voudrait connaître le nombre de carrés de toute
grandeur qui contiennent exactement 2 cases noires.
Combien y a-t-il de tels carrés ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7311
12 mars 2025
Spectacles d’Alain
Alain a noté le nombre de spectacles auxquels il a assisté.
Il multiplie le nombre par 2.
Il additionne 8.
Il divise par 3.
Il soustrait 7.
Le résultat est 13.
À combien de spectacles Alain a-t-il assisté ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7290
5 février 2025
Triangle numérique
Marjo dispose les nombres pairs consécutifs à partir de 4 en un
triangle comme ci-après qui comprend quatre lignes. Elle veut
continuer à écrire les nombres selon le même modèle.
4
6 8
10 12
14
16 18
20
22
Quel sera le terme du milieu de la neuvième ligne ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7289
5 février 2025
Triangles de Constance
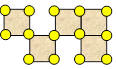
Constance découpe cinq triangles équilatéraux de même grandeur. Elle
les accole côté par côté comme ci-après. Cette figure est formée de
quatre côtés.
Ajoutez quatre triangles pour que la nouvelle figure ait trois
côtés.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7288
5 février 2025
Peurs de Zénon
Zénon
a écrit les trois égalités ci-après dans lesquelles chaque lettre a
une valeur différente. Un groupe de deux lettres correspond à un
nombre de deux chiffres.
P + E = UU
U + R = S
ER + P = RE
Quel nombre correspond à PEURS ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7287
5 février 2025
Égalité
de Gilles
Gilles a représenté 10 avec trois 2 et trois 3. Voici ce qu’il a
écrit :
32 – 23 + 3 – 2 = 10
Représentez 50 avec trois 2 et trois 3, sans utiliser 23.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7286
5 février 2025
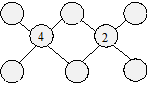
Coins cachés
Dans chaque coin, Reine a placé un jeton numéroté. Elle a multiplié
les numéros de deux jetons de la même rangée et a indiqué le
résultat entre les jetons. Puis elle a effacé les numéros des
jetons.
Quel est le numéro du jeton
de chaque coin ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7265
11 décembre 2024
Bâtonnets de Mireille
Mireille a écrit les chiffres de 2 à 7 avec des bâtonnets.
Combien y a-t-il de nombres de deux chiffres, supérieurs à 50, qui
utilisent 10 bâtonnets pour leur écriture ? |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7264
11 décembre 2024
Grille de
Donald
Donald veut placer chacun des nombres de 3 à 10 dans la grille. La
somme doit être 21 dans chaque ligne, colonne et diagonale de trois
cases voisines. Le 4 est en bonne position.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7263
11 décembre 2024
Dominos de Lucienne
Lucienne choisit huit dominos : (0, 4), (1, 2), (1, 3), (1, 4), (2,
6), (3, 4), (4, 6), (5, 6). Elle veut les placer sur cette grille
pour qu’il y ait 13 points par ligne et par colonne. Quatre
demi-dominos sont en bonne position.
Répartissez les dominos.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7262
11 décembre 2024
Rime de Valère
Valère a écrit cette addition. Chaque lettre représente un chiffre
différent. On sait que M = 4 et U = 9.
B U T + M O T = R I M E
Quelle est la somme ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7261
11 décembre 2024 Addition de Thomas
Thomas a écrit les égalités suivantes.
CINQ + SIX = 75
UN + QUATRE = 84
DEUX + SEPT = 85
TROIS + CINQ = 96
Quelle est la valeur de TROIS + HUIT ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7240
6 novembre 2024
Partage d’élèves
Dans une classe, il y a 27 élèves.
Le double du nombre de filles,
augmenté de 12, est égal à P.
Le triple du nombre de garçons,
augmenté de 6, est aussi égal à P.
Combien y a-t-il de filles et de garçons dans cette classe ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7239
6 novembre 2024
Disposez les autres jetons.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7238
6 novembre 2024
Animaux d’Alexina
Alexina a choisi quatre noms d’animaux. Chaque chiffre représente
une lettre différente.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7237
6 novembre 2024
Cartes de Florent
Dans la grille, Florent a dessiné des cœurs et des trèfles.
Combien y a-t-il
de carrés 2 × 2 qui contiennent exactement un cœur et un trèfle ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7236
6 novembre 2024
Magie de Carlo
Carlo veut former un carré magique avec les nombres de 1 à 25. La
somme des nombres de chaque rangée horizontale, verticale et
diagonale doit être 65. Le nombre donné dans chaque rangée, y
compris dans les diagonales, est la somme des deux cases voisines de
cette rangée.
Formez le carré magique.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7215
2 octobre 2024
En groupes
de trois
Félix s’amuse à grouper trois par trois
les lettres de son prénom
en conservant l’ordre des lettres.
Par exemple, il a trouvé : (F, E, L), (F, E, I), (F, E, X).
Son frère Léonard veut faire de même avec son prénom.
Combien Léonard pourra-t-il former de groupes de trois lettres ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7214
2 octobre 2024
Nombres perdus
Jocelyne a additionné quatre nombres de trois chiffres chacun. Leur
somme est 2181. Le premier est supérieur de 122 au deuxième. Le
troisième est supérieur de 253 au premier. Le quatrième est
supérieur de 81 au troisième.
Quels sont les quatre nombres ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7213
2 octobre 2024
Jetons d’Éliane
Éliane prend 10 jetons. Elle les numérote de 2 à 13, sauf pour 3 et
11. La somme doit être 19 dans chaque rangée horizontale et
verticale de 2 ou 3 cases voisines. Le 2 et le 6 sont en bonne
position.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7212
2 octobre 2024
Jetons d’Arthur
Arthur prend 8 jetons. Elle les numérote de 3 à 12, sauf 7 et 11. La
somme doit être 19 dans chaque rangée de 3 cellules reliées par une
droite. Le 3 et le 8 sont en bonne position.
Disposez les jetons.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7211
2 octobre 2024
Symboles de Jonathan
Dans la grille, Jonathan a dessiné des symboles. Chaque symbole
représente un nombre différent. La somme pour chaque ligne est
donnée, de même que pour les trois premières colonnes.
Quelle est la somme des nombres de la quatrième colonne ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7190
19 juin 2024
Grille de
Karine
Karine veut placer chacun des nombres pairs de 2 à 18 dans la
grille. La somme doit être 30 dans chaque ligne, colonne et
diagonale. Le 2 et le 8 sont en bonne position.
Complétez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7189
19 juin 2024
Poule de Coralie
Coralie a écrit les lettres du mot POULE dans cette grille. On doit
lire ce mot en suivant les lettres qui se touchent horizontalement
et verticalement.
Combien de fois peut-on lire POULE ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7188 19 juin 2024
Veaux de Pierre
Pierre dit à Jacinthe :
« Tu veux savoir combien j’ai de veaux. Voilà !
Je multiplie mon nombre par 2.
Je soustrais 7.
Je divise par 3.
Le résultat est 7. »
Combien Pierre a-t-il de veaux ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7187
19 juin 2024
En morceaux
Félix a préparé cette grille dans laquelle il a écrit des nombres de
3 à 6.
Partagez cette grille en quatre parties égales pour que la somme
soit la même dans chaque partie.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7186 19 juin 2024
Cœur, pique, trèfle
Julie a écrit l’addition suivante. Chaque couleur (cœur, pique,
trèfle) représente un chiffre différent.
À
quel nombre correspond
©ª§
?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7165
15 mai 2024
Contes de Valérie
Valérie a écrit cinq contes.
Chaque conte a exigé quatre pages de plus que le précédent.
En tout, Valérie a couvert 145 pages.
Combien le conte le plus court a-t-il exigé de pages ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7164
15 mai 2024
Grille de Gédéonne
Gédéonne a dessiné la grille rectangulaire 5
´ 7 ci-après.
Elle désire compter les rectangles horizontaux et verticaux 2
´ 4. Des
parties de rectangle peuvent coïncider. Un de ces rectangles est
illustré.
Combien peut-on compter de tels rectangles en tout ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7163
15 mai 2024
Karl et son prénom
Karl a écrit les égalités ci-après dans lesquelles les lettres de
son prénom apparaissent. Chaque lettre représente un chiffre
différent. De plus, L est pair.
Quel nombre correspond à Karl ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7162
15 mai 2024
Tableau de Cédrico
Cédrico a préparé le tableau ci-après qui comprend neuf cases
vides. Il veut y placer chacun des chiffres de 1 à 9. La somme dans
chaque ligne et dans chaque colonne doit être 15.
Remplissez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7161
15 mai 2024
Pommiers de Nathan
Vivien a planté 12 pommiers : 3 en 2020, 4 en 2021, 5 en 2022.
D’une année à l’autre, il plante un pommier de plus. Pour chaque
rangée où il y a un nombre impair de pommiers, l’un d’eux meurt et
n’est pas remplacé.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7130
3 avril 2024
Cases de Ludovic Ludovic veut disposer chacun des nombres de 2 à 10 dans cette figure. La somme des cases reliées par une droite doit être 18. Le 2 et le 3 sont en bonne position.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7129
3 avril 2024
Rectangle d’étoiles
Jocelyne a dessiné six étoiles dans une grille 4 × 6.
Combien peut-on compter de carrés 2
´
2 qui contiennent une seule étoile ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7128
3 avril 2024
Sommes
modifiées
Janine a écrit trois nombres dont la somme est 781.
Remplacez deux chiffres par 2 pour que la somme soit 475. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7127
3 avril 2024
Nouveaux outils
Dans un groupe de jeunes,
9 ont seulement un cellulaire,
7 ont seulement une tablette,
4 ont un cellulaire et une tablette.
Combien y a-t-il d’enfants dans ce groupe ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7126
3 avril 2024
Lettres assorties
Dans la grille, la somme des nombres de chaque rangée horizontale
doit être 18 et celle de chaque rangée verticale doit être 12.
Chaque lettre représente un nombre différent.
Quelle est la valeur de chacune des lettres ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7094
21 février 2024
Groupes de Line
Line a écrit 15 nombres dans cette grille. Sept groupes de 2 nombres
ont chacun une somme de 30, 32 ou 34. Un nombre est solitaire.
Quel est ce nombre ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7093
21 février 2024
Avec calme
Brigitte a donné une valeur inférieure à 10 à chaque lettre du mot
CALME. On sait que :
C + A = 12
L + E = 12
M + E = 13
Quelle est la valeur de CALME ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7092
21 février 2024
Figure de Laura
Laura a inscrit 2 et 4 dans la figure. Elle veut y placer chacun des
nombres de 5 à 10. La somme doit être 17
dans chaque rangée de 3 cellules reliées par une droite.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7091
21 février 2024
Grille
de Réjeanne
Réjeanne veut former un carré magique avec les nombres de 1 à 25. La
somme des nombres de chaque rangée horizontale, verticale et
diagonale doit être 65. Les nombres donnés dans le désordre à droite
doivent apparaître dans chaque rangée correspondante. Les cases
grises doivent recevoir les nombres impairs. Six nombres sont en
bonne position.
Formez le carré magique.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7060
10 janvier 2024
Collections d’éléphants
Léa et Jeannine ont ensemble 14 éléphants.
Jeannine et Germaine ont ensemble 16 éléphants.
Les trois amies ont ensemble 25 éléphants.
Combien chacune a-t-elle d’éléphants ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7059
10 janvier 2024
Égalités de Guillaume
Guillaume a écrit ces deux égalités dans lesquelles chaque symbole
représente un nombre différent.
©
+
§
= 39
25 +
©
=
§
Quelle est la valeur du cœur et du trèfle ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7058
10 janvier 2024
Billes de Magalie
Dans une urne, Magalie a choisi cinq billes
marquées chacune par un nombre : 5, 8, 13, 15 et 20.
Elle a fait des opérations en utilisant
chacun des nombres une seule fois. Voici un exemple :
8 × 15 = 120, 120
¸
20 = 6, 6 + 5 = 11 et 13 – 11 = 2.
Le résultat final est 2.
Combinez ces mêmes nombres pour que le résultat final soit 9.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7057
10 janvier 2024
Cases de Monique
Monique veut placer chacun des nombres de 1 à 10, sauf 7, dans la
figure. La somme doit être 16 dans chaque rangée horizontale et
verticales. Le 6 et le 10 sont en bonne position.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7056
10 janvier 2024
Au tour des triangles
Malik tracé un rectangle dans lequel on trouve des droites qui se
coupent.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7025
29 novembre 2023
Ruches en
opération
Le valet de trèfle possède trois ruches de plus que le valet de
carreau.
Le valet de carreau et celui de pique ont ensemble 15 ruches.
Le valet de cœur possède deux ruches de moins que le valet de
carreau.
Les quatre valets possèdent 30 ruches au total.
Combien chaque valet a-t-il de ruches ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7024
29 novembre 2023
Poulailler de Lyne
Lyne possède moins de 60 poules.
· La somme des chiffres du nombre
est supérieure à 10.
· Le nombre est pair.
· Lyne peut faire des cages de 3
poules et il n’en reste aucune.
Combien Lyne possède-t-elle de poules ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7023
29 novembre 2023
Partage d’Alexis
Alexis a écrit 16 nombres dans la grille. Il demande à son frère de
partager la grille en quatre parties de même forme et de même
grandeur. La somme des nombres doit être la même dans chaque partie.
Faites le partage.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7022
29 novembre 2023
Pentagones de
Denis
Denis
a disposé 10 pentagones en une addition comme ci-après. Chaque
pentagone doit recevoir une valeur différente variant de 0 à 9. Le
premier nombre contient un 7 et le deuxième un 4. De plus, la somme
des deux nombres est 1503.
Quels sont ces deux nombres ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 7021
29 novembre 2023
Grille de José
José a composé un carré magique contenant chacun des nombres de 1 à
25. La somme dans chaque rangée horizontale, verticale et diagonale
doit être 65. José a indiqué autour du carré la somme des 2 cases
voisines dans la même rangée.
Rétablissez le carré.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6990
18 octobre 2023
Dons de Mme Terrier
Mme Terrier se
prépare à déménager.
Elle donne à
une amie le tiers de ses lapins.
À une autre
amie, elle donne le quart de ce qui lui reste.
Elle donne 10
lapins à une troisième amie.
Il lui reste 5
lapins.
Combien Madame
Terrier avait-elle de lapins à l'origine ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6989
18 octobre 2023
Tous pour
50
Kent s’amuse à représenter le nombre 50.
Il choisit des chiffres identiques qui peuvent former des nombres.
Il applique des opérations élémentaires.
Par exemple, avec six 2, il a écrit :
(22
×
2) + 2 + 2 + 2 = 50
ou encore (22 + 2 + 2/2)
× 2.
Trouvez une représentation de 50 avec sept 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6988
18 octobre 2023
Figure d’Ursule
Ursule veut placer chacun des nombres de 3 à 10 dans cette grille.
La somme doit être 18 dans chacune des quatre rangées de deux ou
trois cases. Le 5 est en bonne position.
Placez les nombres dans la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6987
18 octobre 2023
Carreaux de
Luc
Luc a assemblé 30 carreaux en un rectangle 5 × 6 comme ci-après. En
suivant les lignes, il veut tracer des rectangles 2 × 3. Certaines
parties peuvent coïncider.
Combien peut-on compter de rectangles 2 × 3 ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6986
18 octobre 2023
Dominos de Cécile
Cécile prend six dominos :
(0, 6), (1, 1), (1, 6), (2, 5), (2, 6), (3, 4).
Elle veut les placer sur le contour du carré. Il doit y avoir 14
points sur chaque côté. Les deux demi-dominos 2 sont en bonne
position.
Disposez les dominos.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6960
6 septembre 2023
Veaux
affamés
Dans une ferme, il y a trois veaux appelés Coco, Dodo, Lolo.
Chaque veau a mangé une certaine quantité de foin.
Dodo a mangé la moitié de la quantité de Lolo.
Coco a mangé 5 bottes de moins que Dodo.
Au total, 27 bottes de foin ont été mangées par les trois veaux.
Combien Lolo a-t-il mangé de bottes de foin de plus que Coco ? |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6959
6 septembre 2023
Un poulailler revigoré
Germaine a acheté entre 50 et 100 poulets.
Si elle partageait les poulets en groupes de 3, il
en resterait 2.
Si elle partageait les poulets en groupes de 5, il
en resterait 2.
Si elle partageait les poulets en groupes de 9, il
en resterait 2.
Combien Germaine a-t-elle acheté de poulet ? |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6958
6 septembre 2023
Magie de Donatienne Donatienne écrit 2 et 3 dans la figure. Elle veut y placer les nombres de 5 à 10, sauf 8. La somme doit être 18 dans chaque rangée de 3 cellules reliées par une droite.
Complétez la figure. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6957
6 septembre 2023
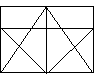
Rectangles de Livia
Livia a tracé cette figure qui contient 20 petits carrés
À
l’exception des petits carrés, combien y a-t-il de carrés de toute
grandeur dans cette figure ? |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6956
6 septembre 2023
Distribution de noisettes
Danika distribue des noisettes à 5 enfants dont les initiales sont
A, B, C, D et E. Elle a écrit ces 5 égalités qui contribuent à
établir le nombre de noisettes de chacun.
Combien chaque enfant recevra-t-il de noisettes ? |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6934
3 juin 2023
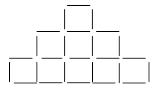
Cure-dents de Donald
Donald a utilisé des cure-dents pour commencer à construire cette
pyramide. Il veut ajouter 3 rangées en dessous tout en respectant la
régularité.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6933
3 juin 2023
Marche d’un bijou
Amanda pose un bijou sur la case 1 de la grille. Ce bijou se déplace
en L comme le cavalier aux échecs. Les 5 premières cases atteintes
sont indiquées.
À la suite de 5, trouvez un chemin qui permet au bijou d’atteindre
toutes les cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6932
3 juin 2023
Lettres de Geneviève
Geneviève a écrit les trois égalités ci-après dans lesquelles chaque
lettre a une valeur différente. Un groupe de deux lettres correspond
à un nombre de deux chiffres.
M + A = CC
C + T = B
AT + M = TA
Quelle est la somme des cinq lettres ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6931
3 juin 2023
Dés de Carole
Carole achète et donne des dés. Chaque mois, elle fait deux
opérations dans cet ordre.
·
Elle achète la moitié du nombre
de dés qu’elle a.
·
Elle donne 7 ou 8 dés afin d’obtenir un nombre pair.
Au bout de quatre mois, Carole a 32 dés.
Combien Carole avait-elle de dés au début ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6899
12 mai 2023
Jetons de Zéphirin
Zéphirin prend 10 jetons. Il les numérote de 3 à 14, sauf pour 5 et
13. La somme doit être 21 dans chaque rangée horizontale et
verticale de 2 ou de 3 cases voisines. Le 3 et le 8 sont en bonne
position.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6898
12 mai 2023
Marche d’un pion
Liette pose un pion sur la case 1 de la grille. La pièce se déplace
en 2 mouvements qui se font en alternance. Le premier mouvement est
celui du cavalier aux échecs, soit en L. Le deuxième mouvement est
un pas horizontal ou vertical. Les 4 premières cases atteintes sont
indiquées.
À la suite de 4, trouvez un chemin qui permet au pion d’atteindre
toutes les cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6897
12 mai 2023
Magie de Jacob
Jacob a écrit 9 et 10 dans la figure. Il veut y placer chacun des
nombres de 1 à 8, sauf 4. La somme doit être 18 dans chaque rangée
de 3 ou de 4 cellules reliées par une droite.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6896
12 mai 2023
Cases grises
Dans cette grille, Denise a noirci 5 cases. Elle veut colorer 7
cases en gris pour qu’il reste une case blanche dans chaque ligne,
chaque colonne et chacune des 2 diagonales.
Trouvez une façon de faire le coloriage.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6864
21 avril 2023
Boules de Nicolas
Nicolas a tracé des carrés de même grandeur. Il dessine une boule à
chaque coin. Il les accole par au moins une boule. Voici un exemple
où 5 carrés exigent 14 boules :
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6863
21 avril 2023
Grille de Sylvio
Sylvio veut écrire les nombres de 2 à 7 sur la première ligne, de 8
à 13 sur la deuxième ligne, de 14 à 20 sauf 17 sur la troisième
ligne. La somme doit être 32 dans chaque colonne. Les cases grises
doivent recevoir des nombres pairs. Quatre nombres sont en bonne
position.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6862
21 avril 2023
Billes de Sébastien
Dans un sac, Sébastien a placé six billes marquées 1, 2, 3, 4 et
5. Il pige en même temps trois billes et il fait la somme des
numéros. Il note la somme et remet les billes dans le sac. S’il
obtient plus d’une fois la même somme, il ne la compte pas.
Combien y a-t-il de sommes impaires possibles ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6861
21 avril 2023
Triangle d’Adèle
Adèle dispose les nombres consécutifs à partir de 5 en un triangle
comme ci-après qui comprend cinq lignes. Elle veut continuer à
écrire les nombres selon le même modèle.
5
6 7
8 9
10
11 12
13
14
15 16
17
18
19
Quel sera le premier terme de la dixième ligne ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6829
30 mars 2023
Un meilleur score
Dans un jeu où la récompense est distribuée en points,
- Fabrice et Élie ont obtenu ensemble 27 points.
- Marielle et Jonas ont obtenu ensemble 30 points.
- Jonas et Élie ont obtenu ensemble 29 points.
- Fabrice et Marielle ont obtenu ensemble 28 points
Qui a eu le meilleur score ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6828
30 mars 2023
Triangles de Clara
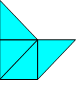
Clara a assemblé quatre triangles rectangles isocèles comme
ci-après. Cette figure a cinq côtés. Il
existe une autre figure qui a cinq côtés avec les mêmes triangles.
Dessinez cette autre figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6827
30 mars 2023
Marche d’un jonc
Sandra pose un jonc sur la case 1 de la grille. Ce jonc se déplace
en L comme le cavalier aux échecs. Les 5 premières cases atteintes
sont indiquées.
À la suite de 5, trouvez un chemin qui permet au jonc d’atteindre
toutes les cases.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6826
30 mars 2023
Trace de Daphnée
Daphnée a écrit neuf groupes de deux lettres dans la grille. Chaque
groupe correspond à un nombre de deux chiffres. Chaque lettre
représente un chiffre différent. La somme des nombres de chaque
ligne, colonne et diagonale est égale à 150. On sait que AE = 42.
Remplissez le carré avec des nombres.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6794
9 mars 2023
Magie de Théo
Théo veut écrire les nombres de 1 à 11 sauf 3 dans les cases de
cette figure. La somme des nombres de 2, 3, 4 cases reliées par une
droite doit être 17. Le 4 et le 11 sont en bonne position.
Complétez la figure.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6793
9 mars 2023
Grille d’Alexis
Alexis veut écrire des nombres de 1 à 5 dans cette grille. Chaque
ligne et chaque colonne doivent contenir des nombres différents.
Les nombres hors de la grille sont la somme des deux nombres voisins
de la même rangée.
Remplissez la grille.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6792
9 mars 2023 Octogone d’Adam
Adam a assemblé 4 petits carrés comme ci-après. Cette figure a huit
côtés.
Assemblez 5 petits carrés pour que la nouvelle figure ait aussi huit
côtés. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6791
9 mars 2023
Marche d’une statuette
Ignace pose une statuette sur la case 1 de la grille. Cette
statuette se déplace en L comme le cavalier aux échecs. Les 4
premières cases atteintes sont indiquées.
À la suite de 4, trouvez un chemin qui permet à la statuette
d’atteindre toutes les cases sauf la noire.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6749 9 février 2023
Dominos de Jolain
Jolain choisit 6 dominos : (1, 2), (1, 4), (2, 2), (2, 5), (3, 3),
(3, 4). Il veut les placer dans le tableau pour que la somme soit
8096. Trois demi-dominos sont en bonne position.
Complétez le tableau.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6748
9 février 2023
Fou en marche
Hélène prend un fou dans la boîte du jeu d’échecs. Elle le place sur
la case 1, puis va jusqu’à la 9. Le fou se déplace d’un pas
obliquement. De plus, il a droit à un
seul pas horizontal ou
vertical.
À la suite de la case 9, déplacez le fou pour qu’il visite toutes
les cases, sauf les noires, une seule fois.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6747
9 février 2023
Carrés de Mathis
Mathis a tracé une grille qui est formée de 28 petits carrés. Il a
noirci 6 petits carrés.
Combien peut-on compter de carrés 3
×
3 qui contiennent exactement 2 petits carrés noirs ?
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
|
# 6746
9 février 2023
Représentation de Laurent
Laurent a représenté 109 avec quatre 1 et quatre 4. Voici ce qu’il a
écrit :
41 + 41 + 41 − 14 = 109
Représentez 200 avec quatre 1 et quatre 4.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||
| Autres divertissements mathématiques | ||||||||||||||||||||||||||||||||||||||||||||||||||