|
(Dessin réalisé au primaire) Contactez-moi : cejean@charleries.net |
Les charleries Bienvenue sur mon blogue, Ce blogue contient des souvenirs, des anecdotes, des opinions, de la fiction, des bribes d’histoire, des récréations et des documents d’archives. Charles-É. Jean
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Propos mathématiques |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3715
2 juin 2017
Divisibilité en magie
Il est bon de
présenter de temps à autre aux élèves des trucs qui relèvent de la
magie. Voici une activité :
Matériel :
tableau, craie ou marqueur, calculatrice chez les élèves
Préparation.
On tire quatre traits sur le tableau. L’enseignant pourra écrire les
chiffres sur ces traits.
L’enseignant
dit :
« Avec vous,
je vais composer des nombres de quatre chiffres qui sont divisibles par
4, c’est-à-dire qu’il n’y pas de reste lorsqu’on fait la division.
Vous allez me
donner un chiffre. [L’enseignant place le chiffre en première position,
soit complètement à gauche.]
À mon tour,
je vais écrire un chiffre. [L’enseignant le place en deuxième position.]
Donnez-moi un
autre chiffre. [L’enseignant le place en troisième position.]
À mon tour,
je vais placer un chiffre en quatrième position. [Si le dernier chiffre
donné est pair, l’enseignant écrit 0, 4 ou 8. Si le dernier chiffre
donné est impair, il écrit 2 ou 6.]
Vérifiez avec
votre calculatrice en divisant ce nombre par 4. »
Exemple. Un
élève choisit 5. L’enseignant le place en première position.
L’enseignant choisit 9 et le place en deuxième position. Un élève
choisit 7 qui est placé en troisième position. L’enseignant choisit 6 et
le place en quatrième position. Le nombre est 5976. Il est divisible par
4.
On doit
suivre les règles suivantes :
• Dans les
trois premières positions, on peut placer n’importe lequel chiffre, sauf
0 au début.
• En
quatrième position, on doit placer un chiffre pair selon la règle
énoncée précédemment.
À la fin,
vous dites aux élèves : « Essayez de trouver le truc. Je vous
l’expliquerai la semaine prochaine. Un élève prendra alors ma place pour
faire la même activité. »
Comme
supplément, l’enseignant pourrait choisir d’écrire les chiffres dans
n’importe quel ordre à la condition d’adapter les règles pour les deux
derniers chiffres. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3670
14 mai 2017
La Fête des Mères
La Fête des Mères qui vise à souligner le dévouement et
l’implication des mères de famille est soulignée dans la plupart des
pays. Au Québec, elle a lieu le deuxième dimanche de mai. Elle arrive au
plus tôt le 8 mai et au plus tard le 14 mai.
Voici trois situations mathématiques inspirées par cette fête :
Situation 1. Connaissant le quantième de la
Fête des Mères en une année, comment trouver le quantième de l’année
suivante ?
Étapes
• Quand l’année cherchée est ordinaire, on soustrait 1 au quantième
donné.
• Quand l’année cherchée est bissextile, on soustrait 2 au
quantième donné.
• Si le résultat est plus petit que 8, on additionne 7.
• Si le résultat est plus grand ou égal à 8, c’est le quantième
cherché
En 2017, cette fête a lieu le 14 mai. Quel sera le quantième en
2018 ? On fait : 14 – 1 = 13. Ce sera le 13 mai en 2017.
En 1999, cette fête a eu lieu le 9 mai. Quel a été le quantième en
2000 ? On fait : 9 – 2 = 7 et 7 + 7 = 14. En 2000, la fête a eu lieu le
14 mai.
Situation 2. Connaissant le jour de la semaine
du 1er janvier d’une année, comment trouver le quantième de
la Fête des Mère en cette même année ?
Étapes
• Quand l’année est ordinaire, le 1er mai sera le jour
de la semaine suivant celui du 1er janvier.
• Quand l’année est bissextile, le 1er mai sera le
deuxième jour de la semaine suivant celui du 1er janvier.
• On identifie le quantième du premier dimanche après le 1er
mai, puis du second dimanche.
En 2018, le 1er janvier sera un lundi. Le 1er
mai sera un mardi. Le premier dimanche sera le 6 et le second le 13. En
2018, la fête sera célébrée le 13 mai.
En 2020, le 1er janvier sera un mercredi. Le 1er
mai sera un vendredi. Le premier dimanche sera le 3 et le second le 10.
En 2020, la fête sera célébrée le 10 mai.
Situation 3. Pour une année donnée du 21e siècle,
comment trouver le quantième de la Fête des Mères ?
Étapes
•
On prend les deux derniers chiffres de
l’année.
•
On divise ce nombre par 4 et on retient le
quotient en ignorant le reste.
•
On additionne les deux derniers chiffres de
l’année et le quotient.
•
On divise la somme par 7 et on conserve
seulement le reste.
• On
soustrait le reste de 14.
Quel sera le quantième en 2025 ?
On 25 ÷ 4 = 6 reste 1. On retient 6. On fait : 25 + 6 = 31. On fait : 31
÷ 7 = 4 reste 3 et 14 – 3 = 11. En 2025, la fête aura lieu le 11 mai,
tout comme, par exemple, en 2014, 2031, 2042 et 2053. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3630
26 avril 2017
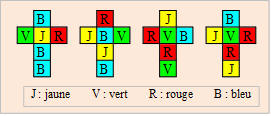
Un solitaire géométrique
Vous pouvez construire un solitaire ou, si vous voulez, un casse-tête
géométrique. Confectionnez quatre cubes de même volume. Placez-les en
une colonne. Vous obtenez ainsi un prisme droit à base carrée. Coloriez
chaque face de côté du prisme d’une seule couleur. Vous avez besoin de
quatre couleurs.
Voici un exemple où on donne les patrons des quatre cubes :
Pour s’aider à assembler les cubes, on commence par compter la fréquence
des couleurs sur chaque facette. Il y a cinq facettes vertes, six
jaunes, six rouges, sept bleues. Seize facettes doivent apparaître sur
les côtés du prisme. Les facettes cachées seront une verte, deux jaunes,
deux rouges et trois bleues. On place les cubes en considérant ces
données. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3570
2 avril 2017
Petits problèmes plaisants
Je publie
dans ce blogue un nouveau livre de ma composition intitulé
Petits problèmes plaisants. Il contient 150 problèmes courts qui
font appel à des connaissances mathématiques et logiques élémentaires.
Les problèmes s’adressent aux amateurs de 9 à 99 ans. Les stratégies de
résolution qui s’appliquent sont généralement à la portée des débutants. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3545
23 mars 2017
Un
nouveau livre
Je publie dans ce blogue un recueil de ma composition intitulé
Jeux de grilles. Il contient 150 problèmes comportant au moins une
grille. Les problèmes font appel à des connaissances élémentaires
d’arithmétique et de logique. On doit composer des carrés magiques, des
carrés latins et des nombres croisés, calculer le nombre de carrés ou de
rectangles dans une grille, transformer des lettres en chiffres,
déplacer des jetons ou encore biffer des nombres qui ont une même
propriété. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
#
3505
7 mars 2017
Trucs de calcul mental
On ne le dira
jamais assez. Le calcul mental est d’une importance capitale. Il n’est
pas nécessairement rapide. Tout comme on montre à l’enfant à attacher
ses chaussures, on doit appuyer sur le calcul mental. Voici trois
exemples où l’enfant peut pratiquer le calcul mental sous un aspect
récréatif :
Premier exercice
On présente à
un jeune enfant une grille de nombres. Il doit repérer les groupes de
deux nombres dont la somme est donnée. En cours de route, il colorie les
cases ou biffe les deux nombres appropriés. Dans cette grille, la somme
est 15.
À la fin, il additionne les nombres qui restent.
Solution. Les nombres qui restent sont 6 et 7. Leur somme est 13.
Les parents peuvent composer des grilles adaptées aux connaissances
de l’enfant.
Deuxième exercice
L’enfant doit compléter la grille pour que la somme soit 17 sur
chaque ligne et dans chaque colonne.
Solution. La grille remplie est :
Troisième exercice
Dans la grille, l’enfant doit trouver combien de couples de nombres
voisins horizontalement et verticalement ont une somme de 15.
Solution. On trouve sept couples. Horizontalement, on a : (7, 8),
(4, 11), (5, 10), (6, 9). Verticalement, on a : (3, 12), (9, 6), (1,
14).
Par surcroit, ce dernier exercice apprend à l’enfant à procéder de
façon systématique.
L’introduction d’un aspect ludique dans ces exercices peut procurer à
l’enfant un certain intérêt, beaucoup plus que s’il devait faire une
série d’additions sur une feuille. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
# 3450
13 février 2017
Cubes magiques
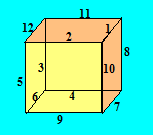
Il existe plusieurs formes de cubes magiques. L’une d’elles a rapport
aux faces. En plaçant 12 nombres sur les arêtes pour que la somme soit
26 sur chaque face, on obtient un cube magique sur les faces. Par
exemple, dans la figure ci-dessous, on a : 12 + 11 + 1 + 2 = 26, 12 + 3
+ 6 + 5 = 26, etc.
Nous donnons une technique simple pour trouver des solutions lorsqu’on
considère quatre faces sur six. Dans la grille ci-après, les losanges
AKBJ, BGCH, LDMC et AEDF sont les quatre faces. Voici comment on
procède :
• On transforme le cube en une grille carrée où les 12 lettres
correspondent aux entiers de 1 à 12. Chaque losange correspond à une
face.
• On fait les combinaisons de deux nombres dont la somme est 13.
1 2
3
4 5
6
12 11
10 9
8 7
• On place en A et B deux nombres dont la somme est 13.
• On place en D et C deux nombres dont la somme est 13.
• On fait (A + D). On écrit les combinaisons possibles de deux nombres
pour cette somme.
• On fait (B + C). On écrit les combinaisons possibles de deux nombres
pour cette somme.
• Dans les combinaisons possibles, on cherche quatre nombres dont la
somme est 26 et qui appartiennent à deux combinaisons de 13. On les
place de façon appropriée en E, F, G et H. Si les quatre nombres
n’existent pas, on revient au début et on fait d’autres essais.
• Si les quatre nombres existent, il reste deux combinaisons. On les
place en J, K, L et M.
Voici une première grille où la somme des nombres est 27 autour de la
case centrale :
Voici une deuxième grille où la somme des nombres est 29 autour de la
case centrale :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour | Accueil | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Suite des propos mathématiques | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||